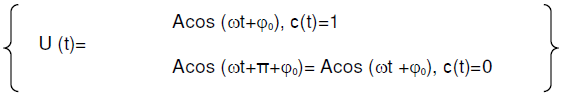2 Введение

Настоящие рекомендации предназначены для инженерно-технического персонала ПЦО, обслуживающего объектовое, ретрансляционное и пультовое оборудование РСПИ, а также специалистов предприятий - изготовителей РСПИ.

В данных рекомендациях дан обзор алгоритмов обмена информацией и методов модуляции в радиоканальных системах передачи извещений, применяемых подразделениями вневедомственной охраны Росгвардии, представлен анализ и сравнительные характеристики современных перспективных видов модуляции.

В технике цифровой связи методы модуляции играют весьма значительную роль. Помимо своей основной функции - преобразования «символ - сигнал» - процесс модуляции является составной частью общего процесса согласования сигнала с характеристиками канала.

Идея способа, позволяющего переносить спектр сигнала в область высоких частот - модулировать высокочастотное радиоволновое колебание, заключается в следующем. В передатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебание. В радиотехнике, и в частности в РСПИ, широкое распространение получили системы модуляции, использующие в качестве несущего простое гармоническое колебание описываемое формулой
U(t)=Usin (ωt+φ), имеющего три свободных параметра:

U - амплитуду, ω - частоту и φ - фазу.

Пусть c(t) низкочастотное сообщение, подлежащее передаче по радиоканалу. Если, по крайней мере, один из указанных параметров изменяется во времени пропорционально передаваемому сообщению, то несущее колебание несёт в себе информацию, заключённую в s(t). Физический процесс управления параметрами несущего колебания называется модуляцией.

Основные принципы построения различных видов модуляции проще всего проанализировать на основе синусоидального сигнала (Рис. 1).

Рис.1. Временная диаграмма гармонического синусоидального сигнала

Таким образом, для передачи информации, а значит модулирования несущего колебания, доступны: амплитуда, частота, фаза.

Наиболее простым видом модуляции является амплитудная модуляция. При передаче информации с применением данного способа модуляции изменению подвергается амплитуда несущего колебания.

Модулированный сигнал для этого вида модуляции имеет вид:

U(t)=A(c(t)+B) cos (ωt+φ),

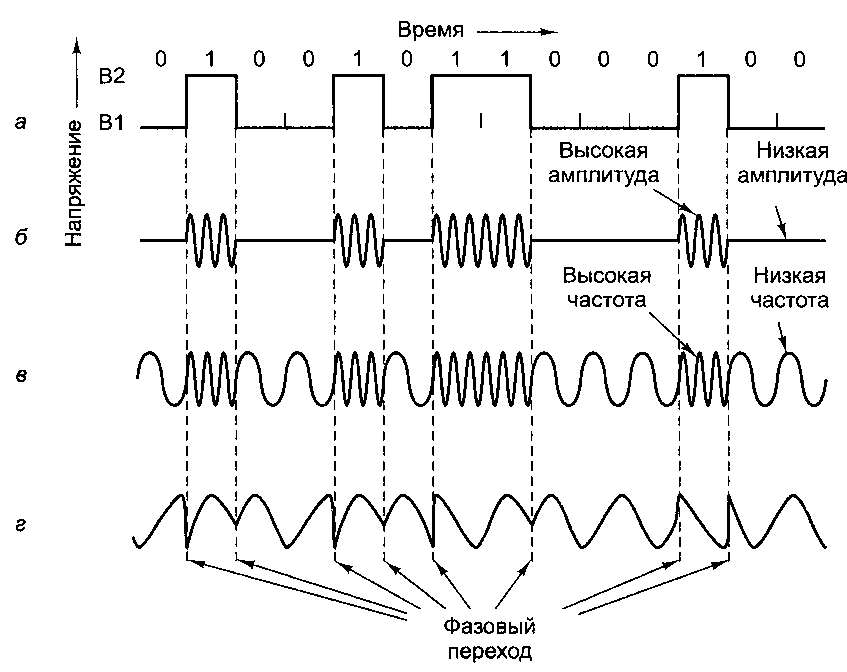
где c(t) - информационный сигнал, А, В и φ - постоянные, В ≥ 0, - ω - несущая частота. Пусть множество возможных значений c(t)= {0,1}, a B = 0. В этом случае модулированный сигнал имеет вид U (t)=A(c(t) cos (ωt+φ), его амплитуда равна 0 при нулевом значении информационного сигнала и А при единичном. Такой тип модуляции называется OOK - (On/Off Keying) модуляция включением/ выключением.

На рисунке 26 показана временная диаграмма амплитудно-модулированного сигнала: информационный «0» передаётся пассивной паузой (отсутствием несущей), а «1» активным пакетом (передачей несущей).

 

Рис. 2. Временные диаграммы различных видов модулированных сигналов

Частотная модуляция является наиболее распространённым видом модуляции радиочастотных сигналов и нашла широкое применение в связи и телефонии.

В случае осуществления частотной модуляции параметром несущего колебания - носителем информации, на который накладывается модулирующее воздействие, является несущая частота ω(t), амплитуда и фаза остаются постоянными.

При частотной модуляции несущая частота ω(t) связана с модулирующим сигналом
c(t)=C0 cos (ω_модt ) зависимостью:

ω(t) = ω₀ + k_ч с (t)

где k_ч - размерный коэффициент пропорциональности между частотой и напряжением.

Частотно - модулированный радиосигнал можно записать в виде формулы:

U(t)=Acos (ω₀t +m_ч sin ω_модt)

где ω₀ - частота несущего колебания в отсутствие ЧМ сигнала;
ω_мод - частота изменения модулирующего сигнала;
m_ч - индекс частотной модуляции.

Индекс частотной модуляции определяется отношением девиации частоты (максимальное изменение частоты несущего сигнала) к частоте модулирующего сигнала:

m_ч = k_ч C₀ /ω_мод

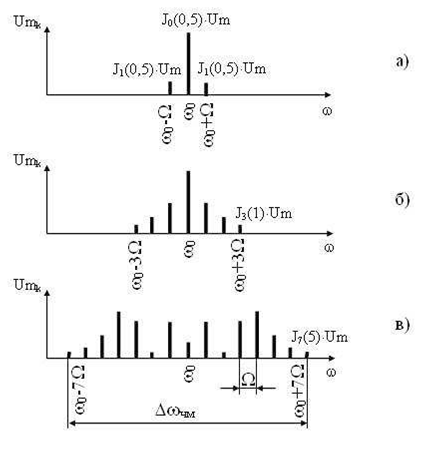
Чем выше индекс модуляции, тем выше помехоустойчивость РСПИ, но вместе с тем и пропорционально расширяется спектр сигнала.

На рисунке 2в показана временная диаграмма сигнала, сформированного методом частотной модуляции.

На рисунке 3 представлены спектры частотно-модулированных сигналов с различными индексами модуляции: a) m=0.5, б) m=1, в) m=5.

В случае, когда информационный сигнал принимает только 2 возможных значения имеет место двоичная частотная модуляция FSK - (Frequency Shift Keying). Информационный сигнал является полярным, т.е. принимает значения {-1,1}, где -1 соответствует значению исходного (неполярного) информационного сигнала 0, а 1 - единице. Таким образом, при двоичной частотной модуляции множеству значений исходного информационного сигнала {0,1} ставится в соответствие множество значений частоты модулированного радиосигнала {ω₀ - ω_d, ω₀ + ω_d}.

Ещё одним видом модуляции радиосигналов является фазовая модуляция. При передаче информации с применением фазовой модуляции в соответствии со значением информационного сигнала изменяется фаза несущего высокочастотного колебания. Фазомодулированный сигнал можно описать формулой:

U (t)=A cos (ωt+φ(t) +φ₀)



Рис. 3. Спектры частотно-модулированного сигнала при различных значениях m

 

Информация при использовании данного метода модуляции кодируется фазой φ(t). Так как при когерентной демодуляции в приёмнике имеется восстановленная несущая Uc (t)=Acos(ωt + φ₀), то путём сравнения сигнала U(t) с несущей вычисляется текущий сдвиг фазы φ(t). Изменение фазы φ(t) взаимно однозначно связано с информационным сигналом c(t). На рис. 2г) показана временная диаграмма фазомодулированного сигнала.

Наиболее простой разновидностью данного вида передачи информации является двоичная фазовая манипуляция BPSK (Binary Phase Shift Keying). Множеству значений информационного сигнала {0,1} ставится в однозначное соответствие множество изменений фазы {0, π}. При изменении значения информационного сигнала фаза радиосигнала изменяется на π. Таким образом, сигнал BPSK можно записать в виде:

 

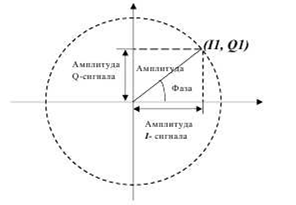
Удобным средством анализа характеристик модулированных сигналов является отображение их с помощью полярных и квадратурных диаграмм в виде сигнальных созвездий.

Известно, что модулированный сигнал с произвольным видом модуляции можно представить в виде:

U(t) = I(t) cos (ω₀t) - Q (t) sin (ω₀t)

где I(t) и Q(t) называются синфазной и квадратурной составляющими модулирующего сигнала соответственно. Низкочастотные сигналы I(t) и Q(t) формируются из исходного сообщения аппаратным или программным способом. Закон, по которому выполняется это преобразование, определяет вид модуляции сигнала. В общем случае при использовании цифровых модулирующих сигналов их количество значений может быть произвольным. Число этих значений называется позиционностью модуляции и обозначается m. 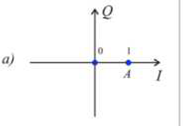В простейшем случае m равно 2. Например, при амплитудной манипуляции значение амплитуды несущей, соответствующее логической «1» будет равно U₀, логическому «0» будет соответствовать нулевая амплитуда (отсутствие сигнала). Соответственно число возможных значений синфазных I(t) и квадратурных Q(t) компонент для формирования U(t) ограничено тем же числом значений. Множество возможных значений квадратурных компонент принято отображать на декартовой плоскости, показанной на рисунке 4, где по оси абсцисс отложены значения синфазной составляющей, а по оси ординат - квадратурной. Такую диаграмму называют сигнальным созвездием.

 

Рис. 4. Изображение синфазной и квадратурных компонент на декартовой плоскости

 

Радиосигнал в этом случае представляется в виде двухмерной точечной диаграммы на комплексной плоскости, точками на которой являются все возможные символы, представленные в геометрической форме. Более абстрактно, на диаграмме отмечены все значения, которые могут быть выбраны данной схемой манипуляции, как точки на комплексной плоскости. Точки на диаграмме часто называют сигнальными точками (или точками созвездия). Они представляют множество модулирующих символов, то есть модулирующий алфавит.

Сигнальное созвездие можно использовать в графическом виде для сравнения помехозащищенности разных видов модуляции. Чем дальше символы на графической плоскости отстоят друг от друга, тем выше помехоустойчивость.

Сигнальные созвездия, полученные в результате исследования радиосигнала, могут использоваться для определения типа манипуляции, рода интерференции и уровня искажений. Ниже представлены сигнальные созвездия для амплитудной модуляции типа ООК (рис. 5 а) и типа ASK (рис. 5 б).

 

Рис. 5. Сигнальные созвездия для модуляции типа ООК и ASK

 

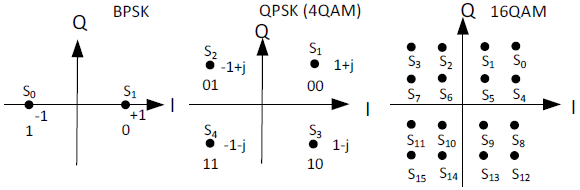
Сигнальные созвездия для различных схем фазовой и амплитудно-фазовой манипуляции сигналов представлены на рис. 6:
- BPSK - двоичная фазовая манипуляция;
- QPSK (4QAM) - четырёхпозиционная амплитудно-фазовая манипуляция;
- 16 QAM - шестнадцатипозиционная амплитудно-фазовая манипуляция.

 

Рис. 6. Сигнальные созвездия для различных схем модуляции

 

Следует отметить, что на сигнальном созвездии положения всех значений символов равноудалены от начала координат. Это означает равенство амплитуд всех символьных колебаний. Требование расположения символов по углам квадрата не является обязательным. Они могут располагаться и по окружности. Следует отметить, что можно позиционность модуляции, делая сдвиги фаз на меньший угол. Тогда в каждом символе будет передаваться большее количество бит и на сигнальном созвездии будет больше точек. Но в этом случае труднее будет в условиях воздействия шумов различать фазовые углы на приеме, поэтому возрастает вероятность ошибочного восстановления при приеме символов.

В случае с методом модуляции 16 QAM необходимо отметить, что разные канальные символы этого сигнала имеют разную энергию. Расстояние между разными сигнальными точками также оказывается различным. В результате вероятность перепутывания символов в приемнике для разных символов оказывается разной.

Один канальный символ такого сигнала может переносить n=log₂m информационных битов. В частности, при m=16 имеем n=4. Поэтому если по-прежнему считать, что длительность одного бита равна то длительность одного канального символа QAM-сигнала равна Tкс = nT_с. Следовательно, при формировании этого сигнала поток информационных битов должен группироваться в блоки по n битов. Каждому блоку должен быть поставлен в соответствие один канальный символ. Установление такого соответствия называется сигнальным кодированием.

Далее >>>